导出exceldemo

题目链接

Yokohama 2018

C - Emergency Evacuation

题目连接

Educational Codeforces Round 85
赛后20分钟A题被hacked了，我没得心态了

A

题目连接

Educational Codeforces Round 59

A

思路

直接拆成2部分，第一部分一个数，第二个部分n个数，考虑相等的情况输入NO，其他为YES

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

#include<bits/stdc++.h>
using namespace std;
#define ll long long
string s;
int main(){
	int q;
	scanf("%d",&q);
	while(q--){
		int n;
		scanf("%d",&n);
		cin>>s;
		if(n==2&&s[0]>=s[1])printf("NO\n");
		else {
			printf("YES\n2\n"); 
		printf("%c ",s[0]);
		for(int i=1;i<n;i++)printf("%c",s[i]);
		printf("\n");
		}
	}
}

题目链接

Codeforces Round #632 (Div. 2)
当时被C题卡了很久，最后20分钟把D的思路想好了却想不到把答案输出的方法，还是思维转变不够快的原因

A

思路

构造题，发现只要构造出

wb
bw

这种[2,2]的形状就可以了

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n,m;
		scanf("%d %d",&n,&m);
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++){
				if(i==0&&j==0)printf("W");
				else printf("B");
			}
			printf("\n");
		} 
	}
}

题目连接

POJ

思路

dp[i][j]表示前i个不同的数，所组成的长度为j的方案数目显然可以得到一个状态转移

但是这样算的话复杂度是O(nm^2)的，复杂度还是会炸，所以考虑优化一下

题目链接

HDU6578

思路

观察到n很小，然后只有4个数字所以我们考虑用DP，来写，状态为dp[i][j][k][l]即把{0,1,2,3}最后出现的位置排序后就是i,j,k,l,例如[0,0,1,1,2,3,1]对应的状态就是dp[2][5][6][1]，然后考虑t+1个数出现的转移方程我们可以得到

dp[i][k][m-1][m]+=dp[i][j][k][m-1]
dp[i][j][m-1][m]+=dp[i][j][k][m-1]
dp[i][j][k][m]+=dp[i][j][k][m-1]
dp[j][k][m-1][m]+=dp[i][j][k][m-1]

思路

首先要明白b数组，其实就是a数组的异或前缀和，那么要怎么保证异或递增？选的数拆成二进制之后肯定需要位数递增才行，所以我们考虑把d拆成2进制，分成很多块儿，就是这样

[1],[10,11],[100,101,110,111],[1000,….],….

分成上面这样的块，然后从这里面找序列就可以了，然后发现这些块的大小是1 2 4 8 16这样的，然后问题就变成了从x个块中分别取1,2,3,4,5~x个数，然后得到的sum，发现这些数都是2的次幂对吧，我们就找它的系数。它的系数应该怎么找的？考虑当$2^k$为最高的位置时，例如$2^2$在第三位的时候，前面可以有$[2^0,2^1,2^2]$这样如果在第二位就有$[2^0,2^2]与[2^1,2^2]$，然后它的系数就是在它前面的和。接下来这样还是不太好求它的系数，但是我们发现如果从低到高的求系数的话，就可以使用前面的信息，例如当我求出$2^1$的系数为2,也就是$[2^0,2^1]以及[2^1]$本身，还有$2^0$的系数为1，也就是[2^0]自身，那么$2^2$的系数就相当于在它前面出现过的序列相加啊，也就是$[2^0,2^1],[2^1],[2^0]$的后面加上$[2^2]$，也就变成$[2^0,2^1,2^2],[2^1,2^2],[2^0,2^2]$所以我们可以直接递增的求出系数6来。当然它可能不一定是整块，最后剩余的部分怎么考虑？前面有x-1块，处理完后，我们就在这些序列的后面直接加上yu的话，也就是多了这些序列*yu的序列，然后还有后面一部分自成序列的情况，也就是再+yu即可。

题目连接

POJ 3450 Corporate Identity

思路

先用后缀数组处理出height数组，然后我们二分最长公共子串的长度，然后再height中找大于这个长度并且不在一个字符串的个数，如果等于n则返回true否则返回false即可。
前期一直TLE不知道为何，换了个板子就过了，也许是我的板子的问题。

题目连接

poj

Height数组

在之前的博客中已经说了后缀数组的具体算法以及如何求出sa数组，但是求出sa之后我们需要学习如何运用sa数组。
第一个运用当然就是height数组了，他表示的意思是

height[i]表示第i小的后缀串与第i-1小的后缀串的最长公共前缀（如图）

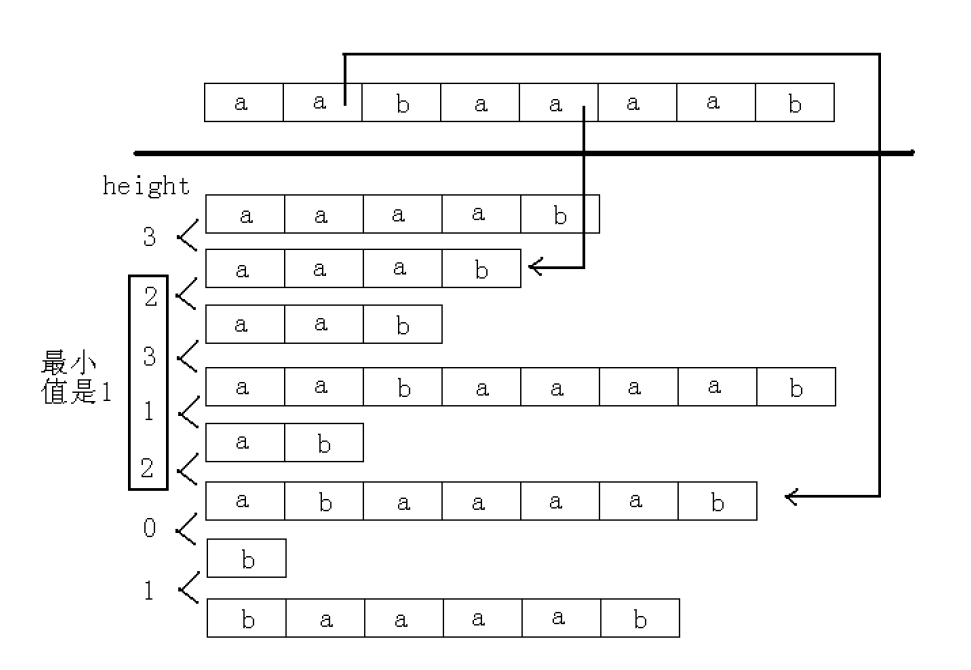
如果能够求出这个数组我们就能够在O(n)时间内求出最长公共子串了。
观察上面那个图，我们发现height有一个规律，它的数是3 2 1 0 3 2 1这样的数，然后我们思考，为什么会这样？我们看第一个3的地方是aabaaaab与aab的最长公共前缀，然后如果我们把它去掉第一个字母，哎就变成abaaaab和ab，是不是有些规律？我们就可以用这个规律来求出我们的height数组。
定义一个数组H[i]=height[rk[i]],也就是从i位置的后缀与在sa数组中排名比他小一名的字符串的最长公共前缀，如果我们从1-n的往后求H[i]，就很惊讶的发现，竟然就是我们刚刚模拟的过程，所以这样我们就可以得到height数组了

1
2
3
4
5

for(int i=1,j=0;i<=n;i++){
	if(j)j--;
	while(s[i+j]==s[sa[rk[i]-1]+j])j++;找出最长的，然后再递减的过程
	h[rk[i]]=j;
}