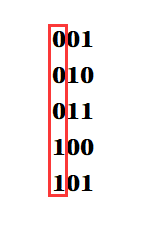异或最小生成树
异或最小生成树就是每个点都有一个权值，而两个点之间连接的边的权值是两个点的异或值，求这个点集合的最小生成树
CF888G
思路
我们会用到Boruvka算法，用上了分治的思想来求最小生成树，但是异或最小生成树呢，则还需要一颗trie树，因为它能够log的查询异或的最小值。
简单解释一下异或最小生成树的步骤
- 对给定的点值排序
- 递归进入子树，从小的子树向大的树合并点集合
- 左子树即当前层为1(或0也可以)的点值插入trie树中
- 在trie树种查询右子树中异或左子树的最小值
- 清空trie树
- 向上递归
例子详解
样例1
5
1 2 3 4 5
1.拆成二进制看
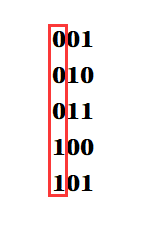
分为了区间[1,3] , [4,5] ,[1,3] 又根据第二位分为[1] , [2,3]。
2.[1]区间的贡献为0，因为不需要连边，[2,3]区间的边的最小贡献为2^3=1。ans+=1,
3.合并[1,3]区间，选择[2,3]之中的一个数去与1异或找到最小值(此处需要trie树，加入答案,ans+=1^3
4.合并[4,5]区间，ans+=4^5
5.合并[1,3],[4,5]区间，这里跟3操作一样，把[1,2,3]插入trie树中，然后枚举[4,5]查询异或最小值即可。ans+=1^5
答案为ans=8
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+10;
ll ans;
int trie[N*30][2],tot,n,a[N];
void insert(int x){
int rt = 0;
for(int i=29;i>=0;i--){
int now = (x>>i)&1;
if(!trie[rt][now])trie[rt][now]=++tot;
rt=trie[rt][now];
}
}
int Search(int x){
int ans = 0,rt=0;
for(int i=29;i>=0;i--){
int now = (x>>i)&1;
if(trie[rt][now]){
rt = trie[rt][now];
}else{
rt = trie[rt][now^1];
ans|=(1<<i);
}
}
return ans;
}
void dfs(int l,int r,int dep){
if(dep==-1||l>=r)return ;
int mid = l-1;
while(mid<r&&((a[mid+1]>>dep)&1)==0)mid++;
dfs(l,mid,dep-1);
dfs(mid+1,r,dep-1);
if(mid==l-1||mid==r)return ;
for(int i=l;i<=mid;i++){
insert(a[i]);
}
int tmp = INT_MAX;
for(int i=mid+1;i<=r;i++){
tmp = min(tmp,Search(a[i]));
}
ans+=(ll)tmp;
printf("%d %d %d\n",l,r,tmp);
for(int i=0;i<=tot;i++){
trie[i][0]=trie[i][1]=0;
}
tot=0;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
sort(a+1,a+1+n);
dfs(1,n,29);
printf("%lld\n",ans);
}
|
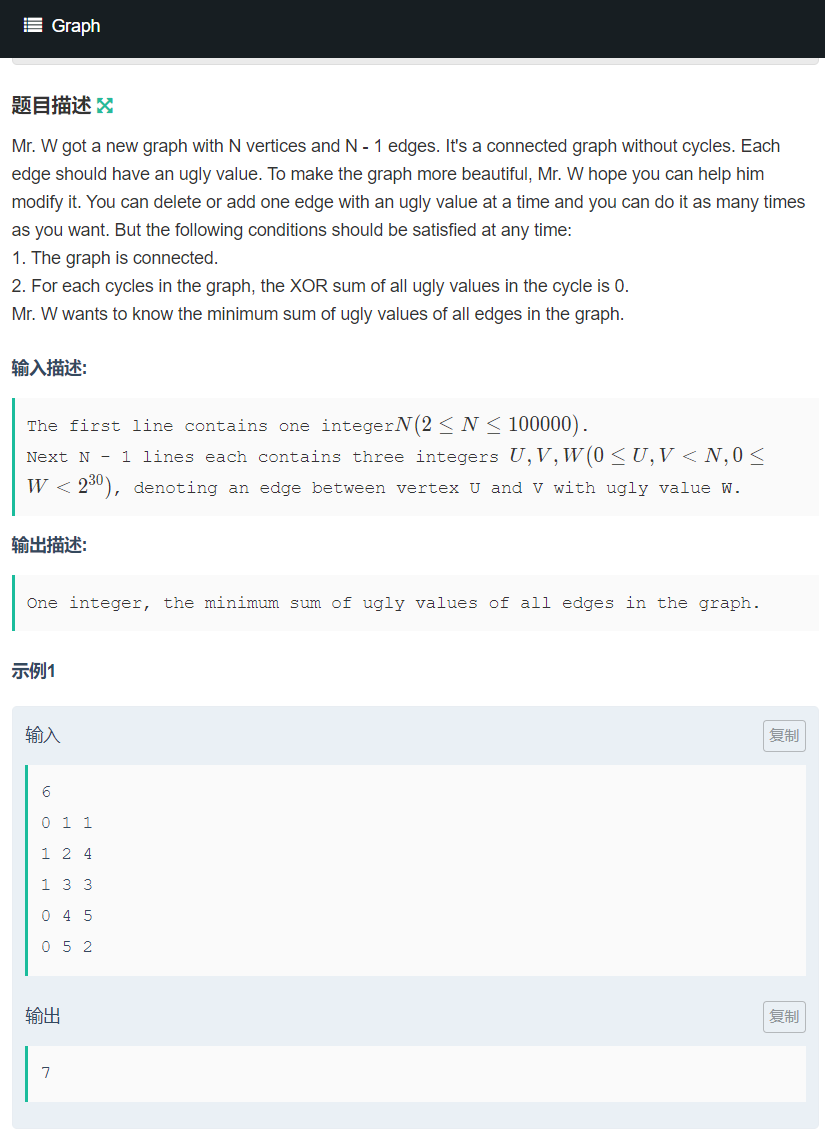
思路
先dfs给每个点赋上一个权值，然后跑一遍异或最小生成树即可
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mk make_pair
const int N = 100010;
ll ans;
int trie[N*30][2],tot,n;
vector<pair<int,int>>g[N];
int val[N];
void add(int u,int v,int w){
g[u].push_back(mk(v,w));
}
void insert(int x){
int rt=0;
for(int i=29;i>=0;i--){
int now = (x>>i)&1;
if(!trie[rt][now])trie[rt][now]=++tot;
rt=trie[rt][now];
}
}
int search(int x){
int res = 0,rt=0;
for(int i=29;i>=0;i--){
int now = (x>>i)&1;
if(trie[rt][now]){
rt = trie[rt][now];
}else{
rt=trie[rt][now^1];
res|=(1<<i);
}
}
return res;
}
void solve(int l,int r,int dep){
if(dep==-1||l>=r)return ;
int mid = l-1;
while(mid<r&&((val[mid+1]>>dep)&1)==0)mid++;
solve(l,mid,dep-1);
solve(mid+1,r,dep-1);
if(mid==l-1||mid==r)return;
for(int i=l;i<=mid;i++){
insert(val[i]);
}
int tmp = INT_MAX;
for(int i=mid+1;i<=r;i++){
tmp = min(tmp,search(val[i]));
}
ans+=(ll)tmp;
for(int i=0;i<=tot;i++){
trie[i][0]=trie[i][1]=0;
}
tot=0;
}
void dfs(int rt,int fa){
for(auto tmp : g[rt]){
if(tmp.first==fa)continue;
val[tmp.first]=val[rt]^tmp.second;
dfs(tmp.first,rt);
}
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<n;i++){
int s,t,v;
scanf("%d %d %d",&s,&t,&v);
s++;
t++;
add(s,t,v);
add(t,s,v);
}
dfs(1,-1);
sort(val+1,val+n+1);
solve(1,n,29);
printf("%lld\n",ans);
}
|