题目连接
poj
Height数组
在之前的博客中已经说了后缀数组的具体算法以及如何求出sa数组,但是求出sa之后我们需要学习如何运用sa数组。
第一个运用当然就是height数组了,他表示的意思是
height[i]表示第i小的后缀串与第i-1小的后缀串的最长公共前缀(如图)
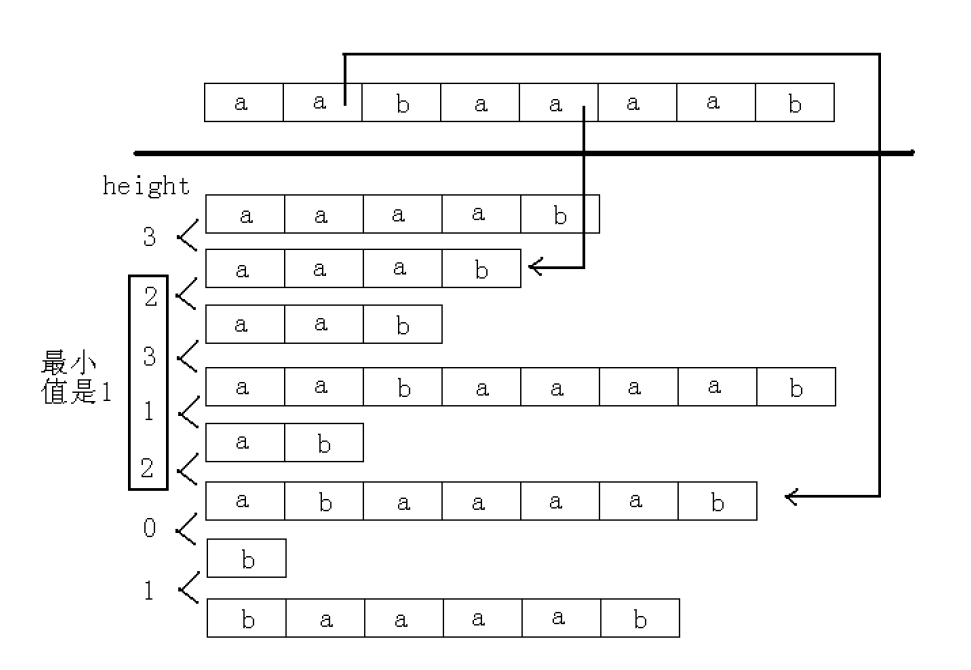
如果能够求出这个数组我们就能够在O(n)时间内求出最长公共子串了。
观察上面那个图,我们发现height有一个规律,它的数是3 2 1 0 3 2 1这样的数,然后我们思考,为什么会这样?我们看第一个3的地方是aabaaaab与aab的最长公共前缀,然后如果我们把它去掉第一个字母,哎就变成abaaaab和ab,是不是有些规律?我们就可以用这个规律来求出我们的height数组。
定义一个数组H[i]=height[rk[i]],也就是从i位置的后缀与在sa数组中排名比他小一名的字符串的最长公共前缀,如果我们从1-n的往后求H[i],就很惊讶的发现,竟然就是我们刚刚模拟的过程,所以这样我们就可以得到height数组了
1
2
3
4
5
| for(int i=1,j=0;i<=n;i++){
if(j)j--;
while(s[i+j]==s[sa[rk[i]-1]+j])j++;找出最长的,然后再递减的过程
h[rk[i]]=j;
}
|
思路
得到height数组后,如何求两个串的最长公共子串?把第二个串连接起来,然后遍历height的,当sa[i]与sa[i-1]记录的位置分别在两个串的时候,就记录答案,这就是最长公共子串
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| #include<cstdio>
#include<string.h>
#include<algorithm>
using namespace std;
#define ll long long
const int N = 1e6+10;
char str[N];
char s[N];
char s1[N];
int n,m;
int rk[N],tp[N],sa[N],tax[N];
int h[N];
void Rsort(){
for(int i=0;i<=m;i++)tax[i]=0;
for(int i=1;i<=n;i++)tax[rk[tp[i]]]++;
for(int i=1;i<=m;i++)tax[i]+=tax[i-1];
for(int i=n;i>=1;i--)sa[tax[rk[tp[i]]]--]=tp[i];
}
bool comp(int *f,int x,int y,int w){return f[x]==f[y]&&f[x+w]==f[y+w];}
void getsa(){
for(int i=1;i<=n;i++)rk[i]=s[i],tp[i]=i;
m=130;
Rsort();
for(int w=1,p=1;p<n;w+=w,m=p){
p=0;
for(int i=1;i<=w;i++)tp[++p]=n-w+i;
for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
Rsort();
swap(tp,rk);
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)
rk[sa[i]]=comp(tp,sa[i],sa[i-1],w)?p:++p;
}
for(int i=1,j=0;i<=n;i++){
if(j)j--;
while(s[i+j]==s[sa[rk[i]-1]+j])j++;
h[rk[i]]=j;
}
}
int main(){
scanf("%s %s",s1,str);
int len1=strlen(s1);
int len2=strlen(str);
for(int i=1;i<=len1;i++){s[i]=s1[i-1];}
for(int i=len1+1;i<=len2+len1;i++){s[i]=str[i-len1-1];}
n=strlen(s+1);
getsa();
int ans = 0;
for(int i=2;i<=n;i++){
if((sa[i]>len1&&sa[i-1]<=len1)||(sa[i]<=len1&&sa[i-1]>len1))ans=max(h[i],ans);
}
printf("%d\n",ans);
}
|
