后缀数组详解

算法的目的

首先，明确我们算法的目的

输入=一个字符串str

输出=一个关于str的后缀排序后的数组，如下图

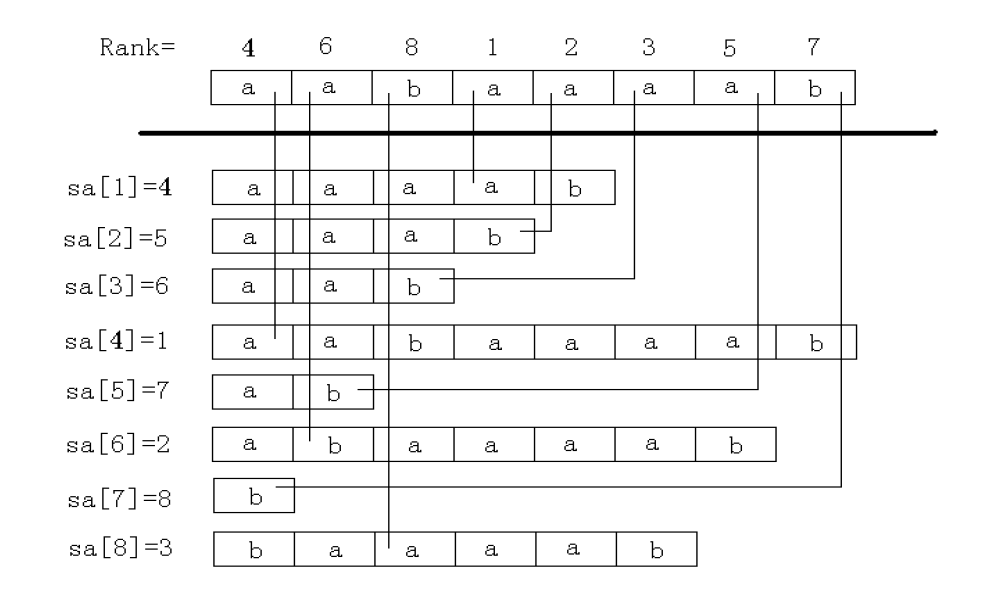
目的就是求出这个sa数组，使得sa[i]=j为第i小的后缀所在的位置

前置知识

倍增

倍增就是每次走倍数次，后面状态的判断可以使用前面判断出的信息来更新，具体的详情百度学习，这里涉及后缀数组的我就给出一张图

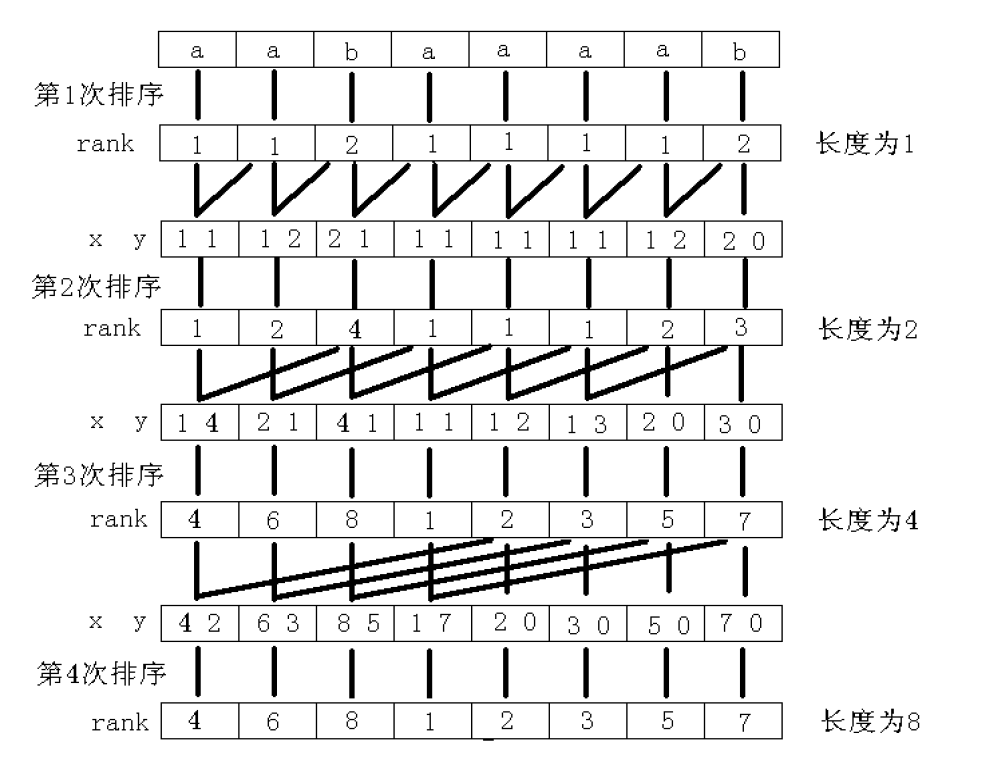
生动一点就是因为都是在同一个字符串上操作，我们需要充分利用我们每一次比较的信息，把它存储起来，以后使用。上图生动一点就是这样，也就是说我们只需要logn次就能够完全比较出一个字符串的所有后缀对吧。

但是还需要排序这样的话每次的复杂度就是O(nlog^2n)，其实已经差不多了，不过仍然有些瑕疵。然后我们考虑到这些数字好像不是很多？因为都是字符，如果我们使用基数排序，就能够将这个复杂度优化到O(nlogn)，所以后缀树组其实就是在字符串上进行倍增+基数排序

算法讲解

4个数组

sa[i]=j表示第i小的字符串是str第j个位置上的后缀

rk[i]=j表示第i个位置上的后缀是第j小，其实与sa是互逆的

tp[i]=j表示第二关键字，基数排序的第二关键字，意义是第i小的字符串是str上的第j个位置

tax[i]表示第i个桶，基数排序所用到的数组

suf[i]没有在代码中出现，但是我讲解的时候表示第i个位置的后缀

还是那个例子，我们是知道rk初始值，直接对字母进行排序即可，然后tp一开始随便定，这里从小到大，然后根据rk为第一关键字，tp为第二关键字，我们能得到sa

	1	2	3	4	5	6	7	8
	a	a	b	a	a	a	a	b
rk	1	1	2	1	1	1	1	2
tp	1	2	3	4	5	6	7	8
sa	1	2	4	5	6	7	3	8

这里解释一下sa[7]=3,表示第7小的字符串是第3个位置上的也就是baaab,然后sa[8]=8表示第8小的字符串是第8个位置上的也就是b，这里很奇怪为什么不对呢？是因为我们只进行了一次，这一次的目的只是把以a开头的和以b开头的顺序确定了下来，但是因为排序关键字仅有2个，所以无法通过更多的信息确定以b开头的后缀的顺序,让我们开始倍增，从1开始，也就是开始比较那些首字母相同的后续的一个，

		1	2	3	4	5	6	7	8
		a	a	b	a	a	a	a	b
第一次	rk	1	1	2	1	1	1	1	2
	tp	1	2	3	4	5	6	7	8
	sa	1	2	4	5	6	7	3	8
第二次	rk	1	2	4	1	1	1	2	3
	tp	8	1	3	4	5	6	2	7
	sa	1	4	5	6	2	7	8	3

rk还是不变，因为我们才刚开始，第一次相当于初始化tp和sa值，然后我们更新tp，这是我们倍增长度为w=1，

for(int w=1,p=1,i;p<n;w+=w,m=p){
    //首先超过后缀不大于w的第二关键字肯定为0 
    for(p=0,i=n-w+1;i<=n;i++)tp[++p]=i;
    //然后根据上一轮的排序求出剩下的第二关键字，从小到大，如果它的位置大于w，说明sa[i]-w这个位置的第二关键字大 
    for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
    Rsort();

也就是把rk第一关键字和tp第二关键字(后缀的第二个字母的大小)，简单解释一下几个tp值，tp[1]=8，是因为第八个位置后面没有字母了，所以显然就是第一小的，然后tp[7]=2,因为suf[2]=abaaaab所以第二个字母是b因此排在第7位，这样tp就能充当我们的第二关键字

	//第一关键字rk，第二关键字tp进行基数排序复杂度O(n) 
for(int i=0;i<=m;i++)tax[i]=0;
for(int i=1;i<=n;i++)tax[rk[tp[i]]]++;
for(int i=1;i<=m;i++)tax[i]+=tax[i-1];
for(int i=n;i>=1;i--)sa[tax[rk[tp[i]]]--]=tp[i];
	//基数排序完毕

我们再次进行基数排序得到sa,这时候发现，那些后缀的前两个字母是aa和ab的顺序已经被确定了，例如sa[4]=6,suf[6]=aa,sa[5]=2,suf[2]=ab顺序已经被确定了。

得到sa之后，我们更新rk数组，如果再次倍增，我们已经不能使用第一个字母作为第一关键字了，所以考虑更新rk，注意，这时候sa中存储的是从1-8，仅仅比较了后缀长度为2的长度，也就是说还有些后缀的顺序是不确定的，我们就需要找出这一部分，我们先把rk放出来，因为更新它的时候还需要用到它，但是这时候第二关键字tp已经没有用了，所以就把rk放在tp中

/把rk数组拿出来，需要求出sa数组，rk[sa[1]]=1是因为第一个位置的rk肯定是1 
swap(tp,rk),rk[sa[1]]=p=1;
//判断当前第一关键字与第二关键字的大小关系，使得没有相等的，若有相等则继续倍增即可 
for(i=2;i<=n;i++)rk[sa[i]]=comp(tp,sa[i],sa[i-1],w)?p:++p;

第二句话很好理解，最小的后缀所在的位置肯定是第一的，这个例子中就是rk[1]=1。

这里解释一个更新rk的例子，此时我们仅考虑长度为2的后缀，当更新sa[2]=4的时候,suf[4]=aa,sa[1]=aa,所以无法判断出在1位置的后缀大还是4后缀大，因此rk[4]=1,再来看一个sa[5]=2,suf[2]=ab,sa[4]=6,suf[6]=aa这样就比较出来，ab>aa的，所以rk[2]=2;实际上，我们从前往后更新，就是前面关键字已经找出来的后缀大小情况，判断是否相等然后得到rank

		1	2	3	4	5	6	7	8
		a	a	b	a	a	a	a	b
第一次	rk	1	1	2	1	1	1	1	2
	tp	1	2	3	4	5	6	7	8
	sa	1	2	4	5	6	7	3	8
第二次	rk	1	2	4	1	1	1	2	3
	tp	8	1	3	4	5	6	2	7
	sa	1	4	5	6	2	7	8	3
第三次	rk	1	2	4	1	1	1	2	3
	tp	7	8	2	3	4	5	6	1
	sa	4	5	6	1	7	2	8	3

接着按照刚刚的说法继续更新tp，sa等！！！

好了，其实后缀数组算法已经结束了，我们不停的做上述操作，知道什么情况？知道p也就是rk中有n个不重复的元素即可，因为每次都是2的倍数，所以复杂度就是O(nlogn).

代码实现

洛谷P3809

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6+10;
char str[N];
char s[N];
int n,m;
int rk[N],tp[N],sa[N],tax[N];
void Rsort(){
		//第一关键字rk，第二关键字tp进行基数排序复杂度O(n) 
	for(int i=0;i<=m;i++)tax[i]=0;
	for(int i=1;i<=n;i++)tax[rk[tp[i]]]++;
	for(int i=1;i<=m;i++)tax[i]+=tax[i-1];
	for(int i=n;i>=1;i--)sa[tax[rk[tp[i]]]--]=tp[i];
		//基数排序完毕
}
	bool comp(int *f,int x,int y,int w){return f[x]==f[y]&&f[x+w]==f[y+w];}
	void getsa(){
	for(int i=1;i<=n;i++)rk[i]=str[i],tp[i]=i;
	m=130;
	Rsort();
	for(int w=1,p=1,i;p<n;w+=w,m=p){
		//首先超过后缀不大于w的第二关键字肯定为0 
		for(p=0,i=n-w+1;i<=n;i++)tp[++p]=i;
		//然后根据上一轮的排序求出剩下的第二关键字，从小到大，如果它的位置大于w，说明sa[i]-w这个位置的第二关键字大 
		for(int i=1;i<=n;i++)if(sa[i]>w)tp[++p]=sa[i]-w;
		Rsort();
		//把rk数组拿出来，需要求出sa数组，rk[sa[1]]=1是因为第一个位置的rk肯定是1 
		swap(tp,rk),rk[sa[1]]=p=1;
		//判断当前第一关键字与第二关键字的大小关系，使得没有相等的，若有相等则继续倍增即可 
		for(i=2;i<=n;i++)rk[sa[i]]=comp(tp,sa[i],sa[i-1],w)?p:++p;
	}
	}
int main(){
	scanf("%s",s);
	n=strlen(s);
	for(int i=0;i<n;i++)str[i+1]=s[i];
	getsa();
	for(int i=1;i<=n;i++)
	if(i==1)printf("%d",sa[i]);
	else printf(" %d",sa[i]);
}