J A+B problem
题目描述

思路
用stoll转换成数字后相加,然后倒序输出
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
string a,b;
cin>>a>>b;
reverse(a.begin(),a.end());
reverse(b.begin(),b.end());
long long A=0;
long long B=0;
A = stoll(a);
B = stoll(b);
long long ans = A+B;
bool ok = false;
while(ans)
{
if(ans%10!=0)
{
ok=true;
}
if(ans%10==0&&ok==false)
{
ans/=10;
continue;
}
printf("%d",ans%10);
ans/=10;
}
cout<<endl;
}
}
|
D Number
题目描述

思路
首先有一个结论,3次以及3次以上的多项式一定可以约分,但需要包含复数域。所以这题大于3的时候和0,1的时候就不用考虑了,只剩下二次多项式,用判别式判断就好了
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<bits/stdc++.h>
using namespace std;
const int maxn = 30;
long long a[maxn];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
for(int i=n;i>=0;i--)
{
scanf("%lld",&a[i]);
}
if(n==0||n==1)
{
printf("Yes\n");
continue;
}
if(n>=3)
{
printf("No\n");
continue;
}
long long zeta = 1ll*a[1]*a[1]-1ll*4*a[0]*a[2];
if(zeta>=0)
{
printf("No\n");
}
else printf("Yes\n");
}
}
|
B Irreducible Polynomial
题目描述

思路
位数不够就补0,位数小于当前位数就无解,位数等于素数位数就输出当前素数
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<bits/stdc++.h>
using namespace std;
int cal(int x)
{
int ans = 0;
while(x)
{
ans++;
x/=10;
}
return ans;
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
int num = cal(m);
if(num>n)
{
printf("T_T\n");
}
if(num==n)
{
printf("%d\n",m);
}
if(num<n)
{
string s(n-num,'0');
cout<<m<<s<<endl;
}
}
|
A String
题目描述
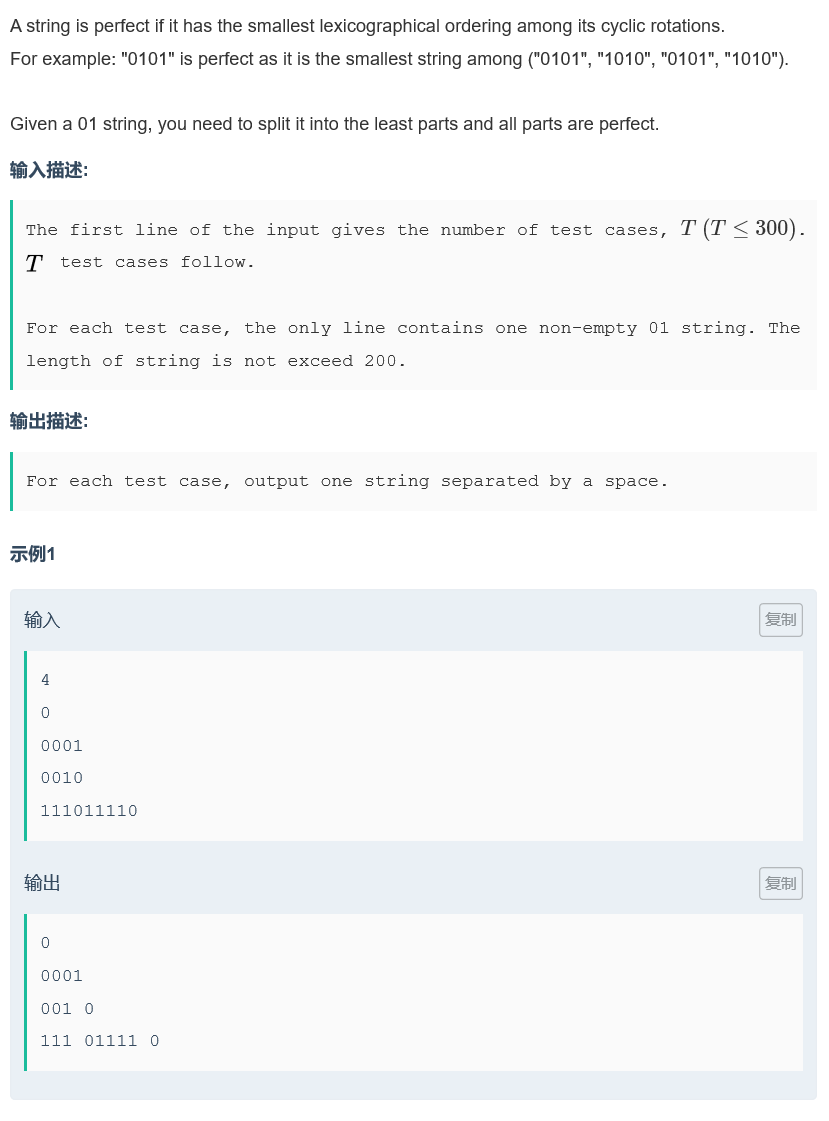
思路
因为长度只有200,所以直接暴力每次从后往前搜满足题意的字符串即可。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include<bits/stdc++.h>
using namespace std;
string si;
bool check(string s)
{
string s1 = s;
for(int i=0;i<s.size();i++)
{
s+=s[0];
s.erase(s.begin());
if(s<s1)return false;
}
return true;
}
void solve(int x)
{
for(int i=si.size()-x;i>=1;i--)
{
string su = si.substr(x,i);
if(check(su))
{
if(su.size()==si.size()-x)
{
cout<<su<<endl;
return;
}
else
{
cout<<su<<" ";
solve(x+i);
return ;
}
}
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
cin>>si;
solve(0);
}
}
|



